 DE
DE

Herausforderung #7 wird um eine zusätzliche Woche verlängert und stellt nun die finale Herausforderung von Parkour Survival 2025 dar.
Herausforderung #8 wird abgesagt, und die Teams, die Herausforderung #7 erfolgreich abschließen, werden zu den offiziellen Gewinnern des Turniers erklärt.
Seit seinem Neustart Mitte August hat Parkour Survival die Kreativität, Teamarbeit und Präzision der Spieler auf ein neues Niveau gehoben. Wir sind beeindruckt von dem Können und Engagement aller Teilnehmer und gespannt darauf, wer sich an die Spitze setzen und die legendäre Farbe „Blaze-Farbe“ gewinnen wird. Vielen Dank an alle, die teilgenommen und dieses Event zu etwas ganz Besonderem gemacht haben – lasst uns das Ganze erfolgreich zu Ende bringen, Panzerfahrer!

Daten: Vom 10. Oktober um 4 Uhr BZ bis 24. November 3 Uhr BZ.
Schauen wir uns die Details an:
Wie man Spieler einlädt:
“Eingeladene” sind Spieler, die Ihr, wie der Name schon sagt, zum Spiel einladet.
Um einen Spieler zu Eurem Eingeladenen zu machen, müsst Ihr:
Schritt 1 Mindestens den Rang eines Unteroffizier haben
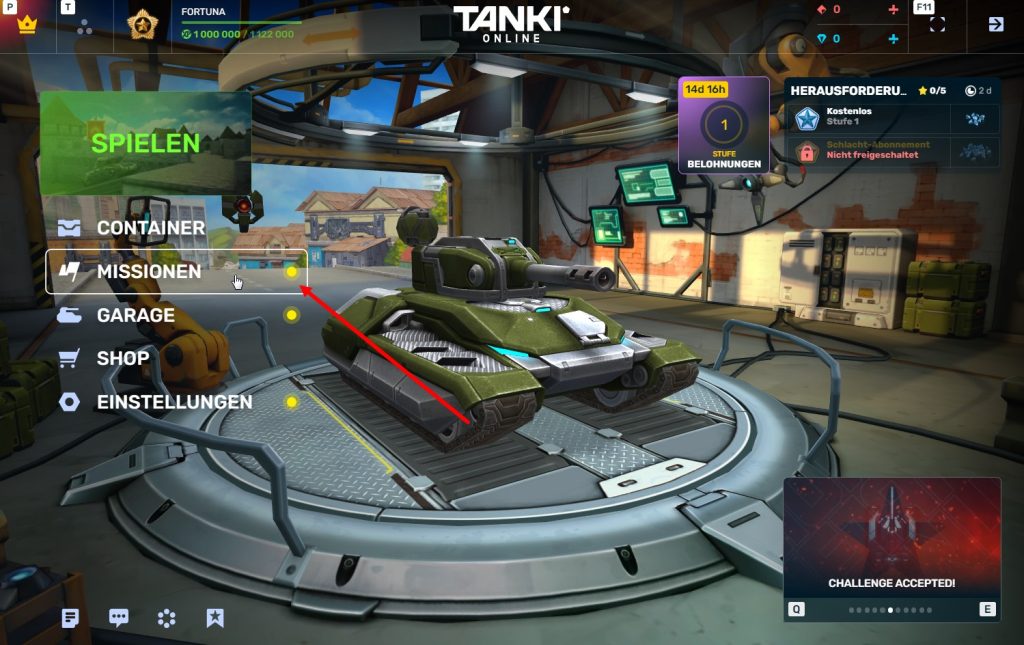
Schritt 2 Euch ins Spiel einloggen und zum Missionsmenü gehen
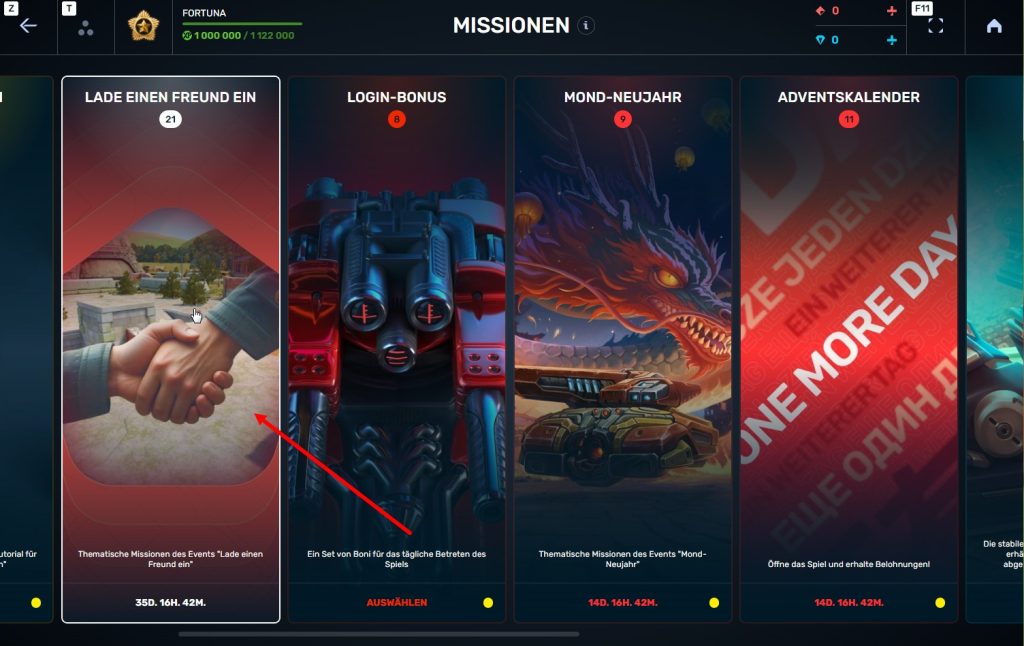
Schritt 3 Die Rubrik „Lade einen Freund ein“ öffnen
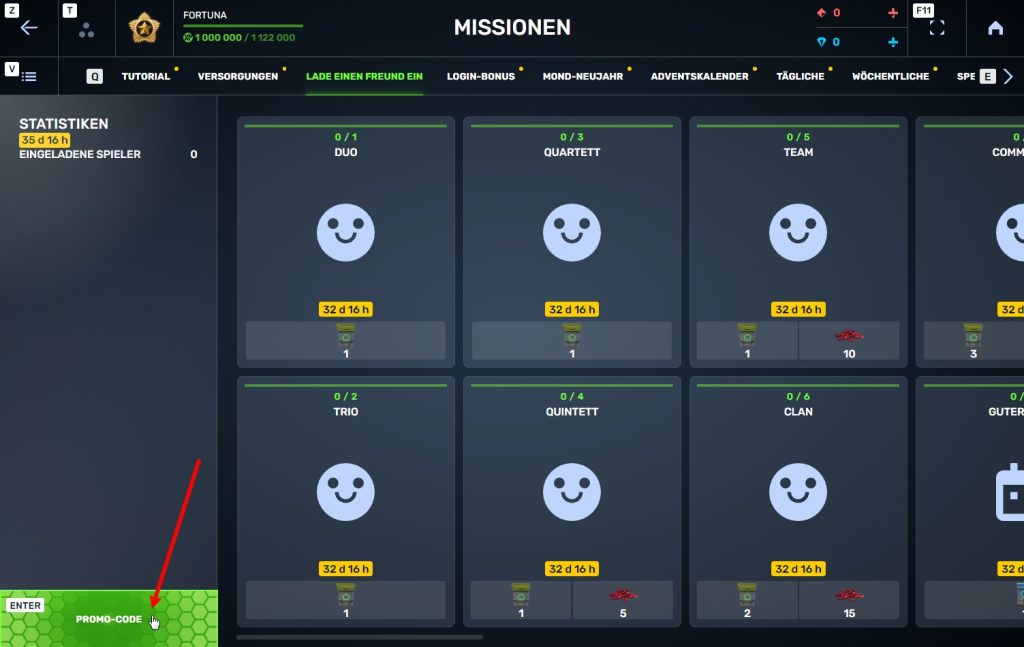
Schritt 4 Einen Promo-Code generieren
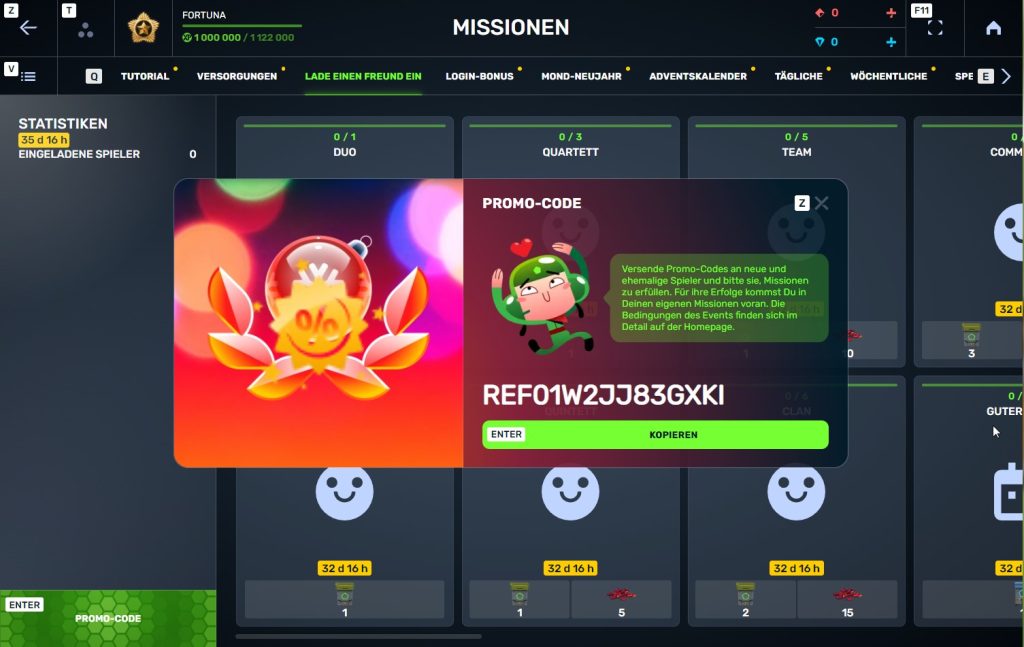
Schritt 5 Diesen Promo-Code mit Personen teilen, die Ihr zum Spiel einladen möchtet und ihnen erklären, wie sie ihn aktivieren können (mehr dazu unten)
Wer kann von Euch eingeladen werden?
- Spieler, die sich zwischen dem 10. Oktober um 4 Uhr BZ und dem 24. November um 3 Uhr BZ registriert haben
- Spieler, die sich zuletzt vor 4 Uhr BZ am 25. August angemeldet haben
Die Aktivierung von Promo-Codes ist ab dem Rang “Soldat” möglich.
Was bekomme ich, wenn ich andere Spieler einlade?
- Nachdem Ihr Eure individuelle Einladung in Form eines Promo-Codes generiert habt, müsst Ihr sie an Eure Freunde und Bekannte senden.
- Als nächstes seht Ihr eine spezielle Rubrik mit Missionen.
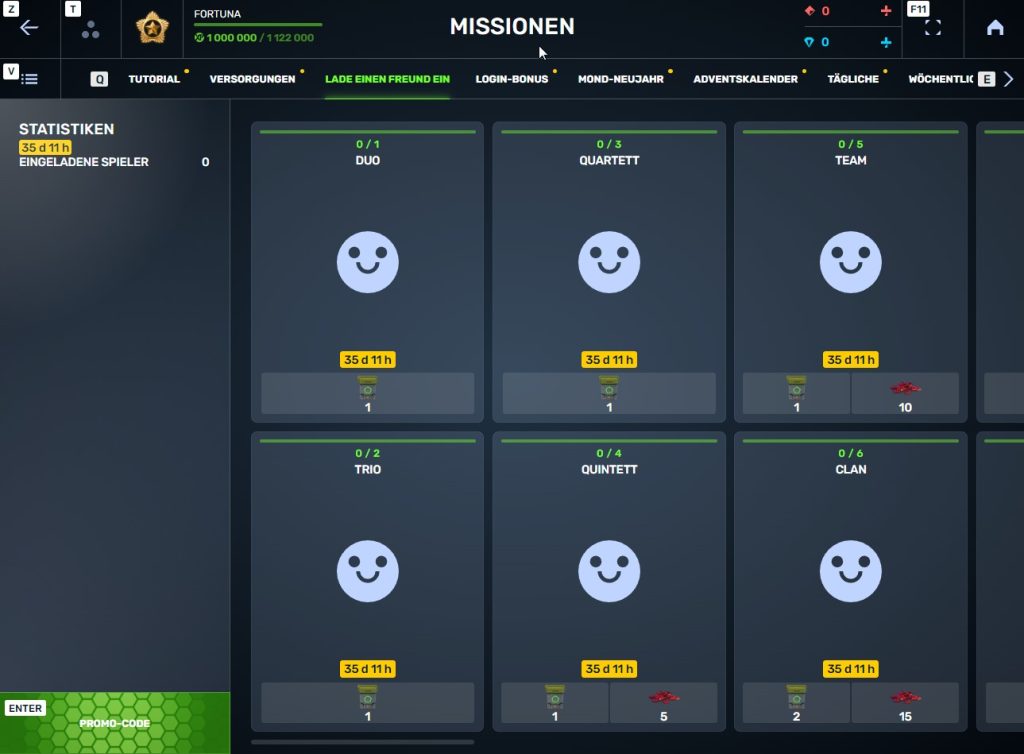
3. Die Spieler, die Ihr eingeladen habt, erhalten, sobald sie Euren Promo-Code aktiviert haben, eigene Spezialmissionen in der Kategorie „Missionen vom Freund“. Danach müsst Ihr nur noch den Spielfortschritt der eingeladenen Spieler verfolgen und Preise für Missionen sammeln.
Missionen für diejenigen, die einladen
Es gibt zwei Arten von Missionen zum Einladen von Spielern. Bei der ersten Art erhaltet Ihr Belohnungen für Spieler, die gerade Euren Promo-Code aktiviert haben. Bei der zweiten Art erhaltet Ihr Belohnungen, sobald Eure eingeladenen Spieler die erforderlichen Missionen abgeschlossen haben.
aufgabe
Lade 1 Spieler zum Spiel ein
belohnung

GEWÖHNLICHER SCHLÜSSEL
Erfahrungspunkte
aufgabe
Lade 2 Spieler zum Spiel ein
belohnung

GEWÖHNLICHER SCHLÜSSEL
Erfahrungspunkte
aufgabe
Lade 3 Spieler zum Spiel ein
belohnung

GEWÖHNLICHER SCHLÜSSEL
Erfahrungspunkte
aufgabe
Lade 4 Spieler zum Spiel ein
belohnung

gewöhnlicher schlüssel

rubine
Erfahrungspunkte
aufgabe
Lade 5 Spieler zum Spiel ein
belohnung

gewöhnlicher schlüssel

rubine
Erfahrungspunkte
aufgabe
Lade 6 Spieler zum Spiel ein
belohnung

gewöhnlicher schlüssel

rubine
Erfahrungspunkte
aufgabe
Lade 7 Spieler zum Spiel ein
belohnung

gewöhnlicher schlüssel

rubine
Erfahrungspunkte
aufgabe
Eingeladene Spieler haben 10 Missionen des Empfehlungsevents abgeschlossen
belohnung

seltener schlüssel
Erfahrungspunkte
aufgabe
Eingeladene Spieler haben 20 Missionen des Empfehlungsevents abgeschlossen
belohnung

seltener schlüssel
Erfahrungspunkte
aufgabe
Eingeladene Spieler haben 30 Missionen des Empfehlungsevents abgeschlossen
belohnung

seltener schlüssel

rubine
Erfahrungspunkte
aufgabe
Eingeladene Spieler haben 40 Missionen des Empfehlungsevents abgeschlossen
belohnung

seltener schlüssel

rubine
Erfahrungspunkte
aufgabe
Eingeladene Spieler haben 50 Missionen des Empfehlungsevents abgeschlossen
belohnung

seltener schlüssel

rubine
Erfahrungspunkte
aufgabe
Eingeladene Spieler haben 60 Missionen des Empfehlungsevents abgeschlossen
belohnung

seltener schlüssel

rubine
Erfahrungspunkte
aufgabe
Eingeladene Spieler haben 80 Missionen des Empfehlungsevents abgeschlossen
belohnung

seltener schlüssel

rubine
Erfahrungspunkte
aufgabe
Eingeladene Spieler haben 1 Supermission des Empfehlungsevents abgeschlossen
belohnung

epischer schlüssel
Erfahrungspunkte
aufgabe
Eingeladene Spieler haben 2 Supermissionen des Empfehlungsevents abgeschlossen
belohnung

epischer schlüssel

rubine
Erfahrungspunkte
aufgabe
Eingeladene Spieler haben 3 Supermissionen des Empfehlungsevents abgeschlossen
belohnung

epischer schlüssel

rubine
Erfahrungspunkte
aufgabe
Eingeladene Spieler haben 4 Supermissionen des Empfehlungsevents abgeschlossen
belohnung

epischer schlüssel

rubine
Erfahrungspunkte
aufgabe
Eingeladene Spieler haben 5 Supermissionen des Empfehlungsevents abgeschlossen
belohnung

epischer schlüssel

rubine
Erfahrungspunkte
aufgabe
Eingeladene Spieler haben 6 Supermissionen des Empfehlungsevents abgeschlossen
belohnung

epischer schlüssel

rubine
Erfahrungspunkte
aufgabe
Eingeladene Spieler haben 7 Supermissionen des Empfehlungsevents abgeschlossen
belohnung

epischer schlüssel

rubine

LEGENDäRer schlüssel
Wie funktioniert es für die Eingeladenen?
Nachdem ein Eingeladener eine Promo-Code-Einladung von Euch erhalten hat, muss er:
Schritt 1 Im Spiel registrieren (oder sich anmelden bei einem vorhandenen Account, wenn er die Kriterien erfüllt)
Schritt 2 Den Rang „Soldat“ zu erlangen, wird nicht lange dauern

Schritt 3 Den Shop öffnen
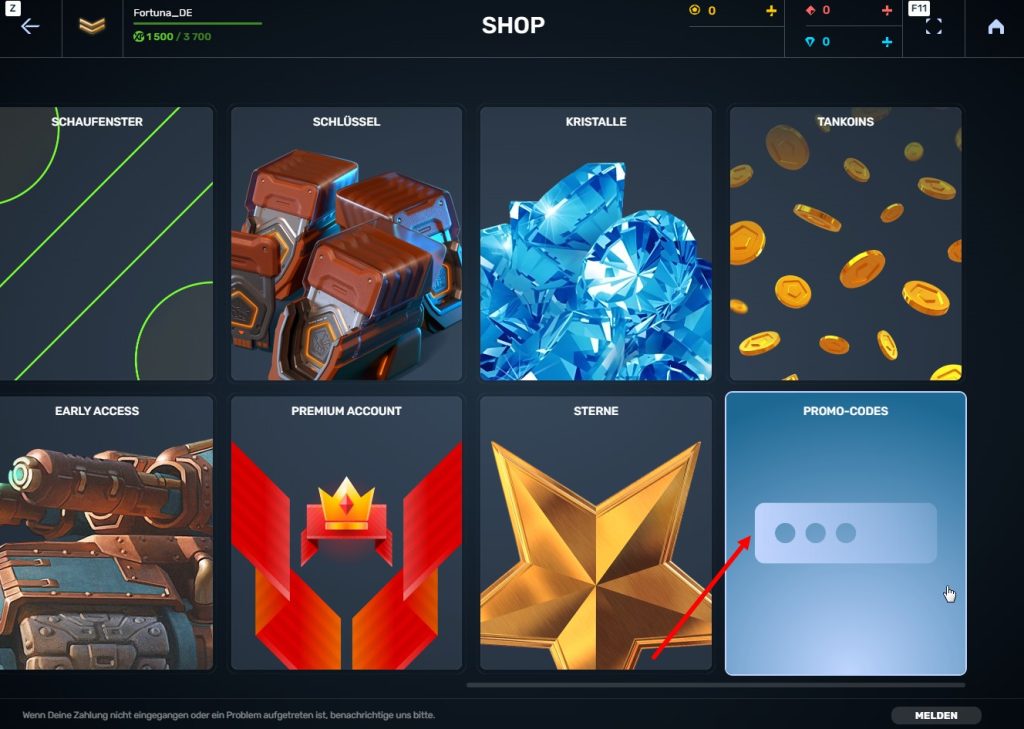
Schritt 4 Zum Abschnitt „Promo-Codes“ gehen
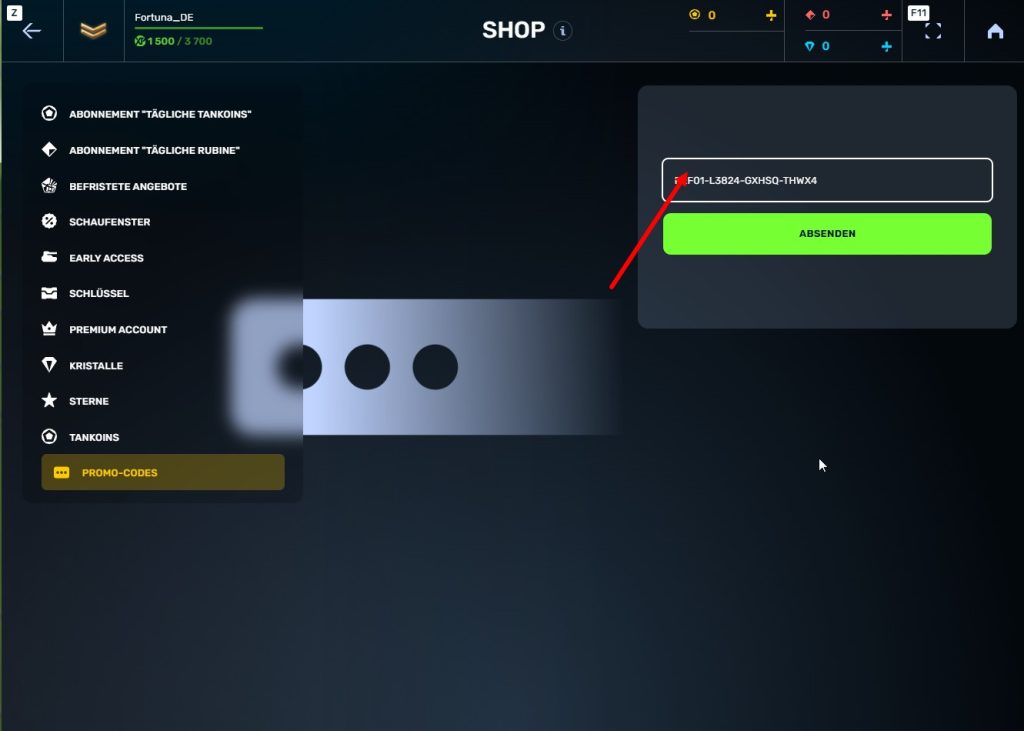
Schritt 5 Den Promo-Code aktivieren
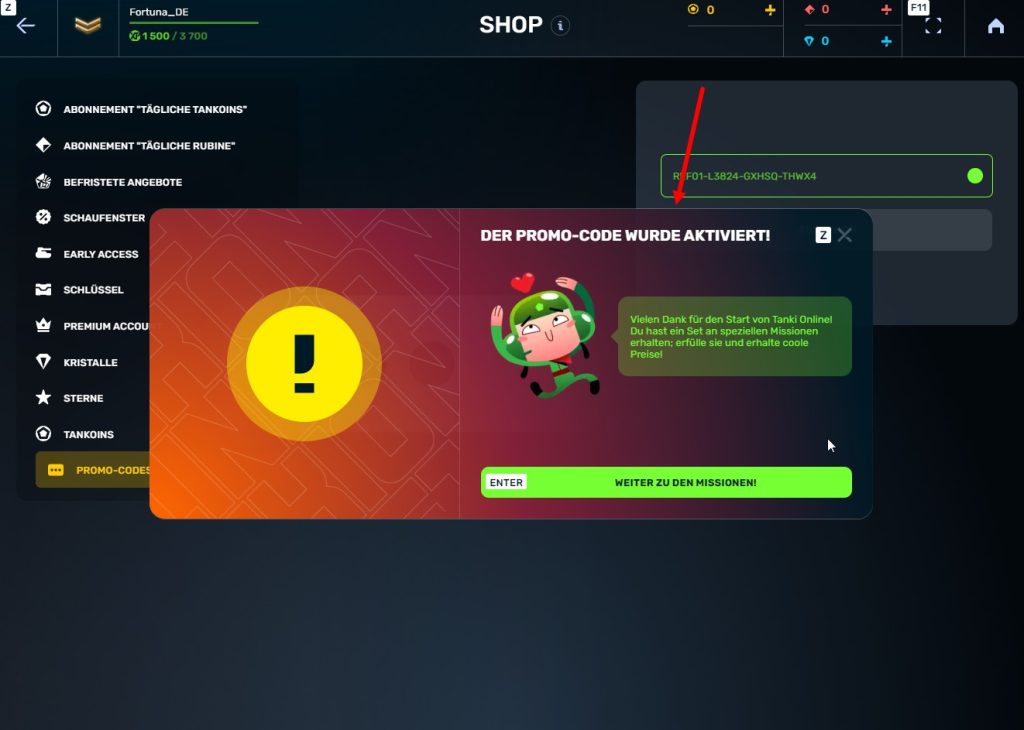
Schritt 6 Den Button „Weiter zu Missionen!“ klicken
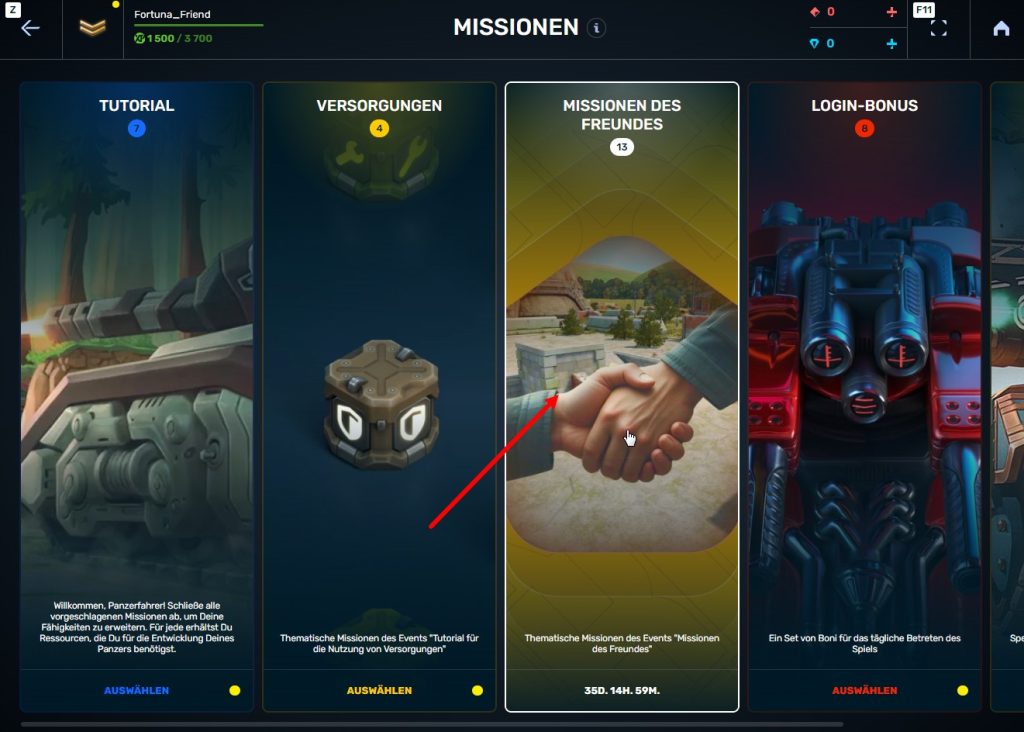
Schritt 7 Als Nächstes gelangt man zur Liste „Missionen von Freunden“ in der Rubrik, wo spezielle Empfehlungsmissionen angezeigt werden
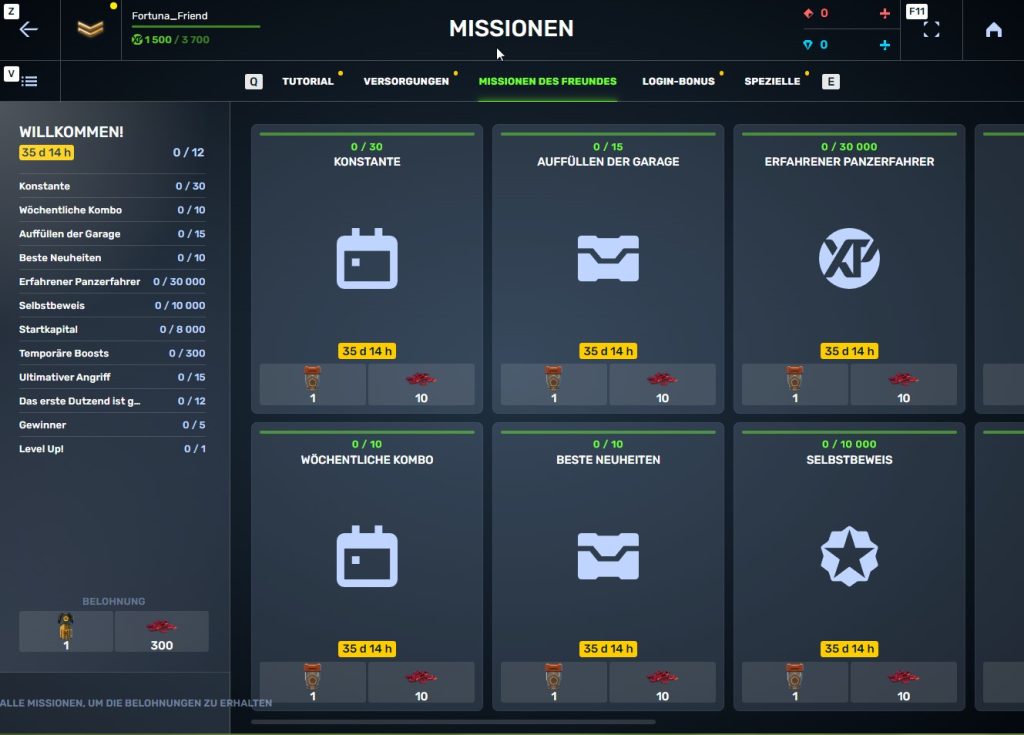
Schritt 8 Missionen abschließen und die Belohnungen sammeln
Boni für das Abschließen von Missionen für die Eingeladenen:
aufgabe
Supermission. Beende alle Empfehlungsmissionen.
belohnung

rubine

LEGENDäRer schlüssel
aufgabe
Beende 30 tägliche Missionen
belohnung

epischer schlüssel

rubine
Erfahrungspunkte
aufgabe
Beende 15 wöchentliche Missionen
belohnung

epischer schlüssel

rubine
Erfahrungspunkte
aufgabe
Öffne 15 Gewöhnliche Container.
belohnung

epischer schlüssel

rubine
Erfahrungspunkte
aufgabe
Öffne 10 Epische Container.
belohnung

epischer schlüssel

rubine
Erfahrungspunkte
aufgabe
Erspiele 30 000 Erfahrungspunkte.
belohnung

epischer schlüssel

rubine
Erfahrungspunkte
aufgabe
Erspiele 15 000 Reputationspunkte.
belohnung

epischer schlüssel

rubine
Erfahrungspunkte
aufgabe
Verdiene 10 000 Kristalle.
belohnung

epischer schlüssel

rubine
Erfahrungspunkte
aufgabe
Benutze 300 mal eine Versorgung.
belohnung

epischer schlüssel

rubine
Erfahrungspunkte
aufgabe
Benutze 15 mal den Overdrive.
belohnung

epischer schlüssel

rubine
Erfahrungspunkte
aufgabe
Beende 20 Schlachten.
belohnung

epischer schlüssel

rubine
Erfahrungspunkte
aufgabe
Beende 5 Schlachten im Gewinnerteam.
belohnung

epischer schlüssel

rubine
Erfahrungspunkte
aufgabe
Erhalte einen neuen Rang
belohnung

epischer schlüssel

rubine
Erfahrungspunkte
Ladet Eure Freunde ein und erhaltet Belohnungen!

Ihr erinnert Euch sicherlich, dass Spieler auf der Nintendo Switch™ seit dem erstmaligen Release im März 2025 lediglich mit neuen, separaten Accounts spielen konnten. Von nun an habt Ihr aber kompletten Zugang zu Eurem Hauptaccount, mit welchem Ihr zuvor in der PC- oder Android-Version gespielt habt!
Wie loggt man sich in seinen Account ein?
Ihr müsst das Spiel auf der Nintendo Switch™ öffnen und zuerst Euren dortigen Account abmelden. Das geht folgendermaßen:
- Geht in die Einstellungen im Spiel.
- Wählt den Bereich “Account” aus.
- Drückt auf den Button “Von diesem Account abmelden”.
Hiernach erscheint ein Login-Formular, in welchem Ihr Euch mit Eurem Benutzernamen und Passwort Eures Accounts autorisieren könnt, den Ihr auf einer anderen Plattform erstellt hattet.
Kämpft auf jedem beliebigen Gerät in Schlachten! Erzählt Euren Panzer-Kollegen von dieser Neuigkeit – wir sehen uns auf dem Schlachtfeld!

Dauer des Events: Vom 3. Oktober bis zum 16. Oktober (jeweils 4 Uhr BZ).
Wie spielt man mit?
Um am Event “Schiffe versenken” teilzunehmen, müsst Ihr Kontrakte und Spezielle Missionen im Spiel erledigen. Bei Beendigung dieser erhaltet Ihr Energie, mit welcher Ihr gegnerische Panzer auf dem Spielfeld angreifen könnt.
Schlacht
Für die gesamte Dauer des Events werdet Ihr jeden Tag in speziellen Schlachten auf der Event-Website kämpfen können.
In der Schlacht hat jeder Spieler eine Basis, eine bestimmte Menge an Panzern sowie eine Mine, die auf dem Spielfeld beliebig verteilt werden können:





Bevor Ihr eine Schlacht startet, müsst Ihr Panzer auf dem Spielfeld platzieren und könnt dabei herausfinden, wie sie sich (auch auf den gegnerischen Feldern) anordnen lassen.

Nach Positionierung der Panzer folgt das Hauptspiel, in welchem Ihr Felder mit zufällig platzierten gegnerischen Panzern erhaltet.
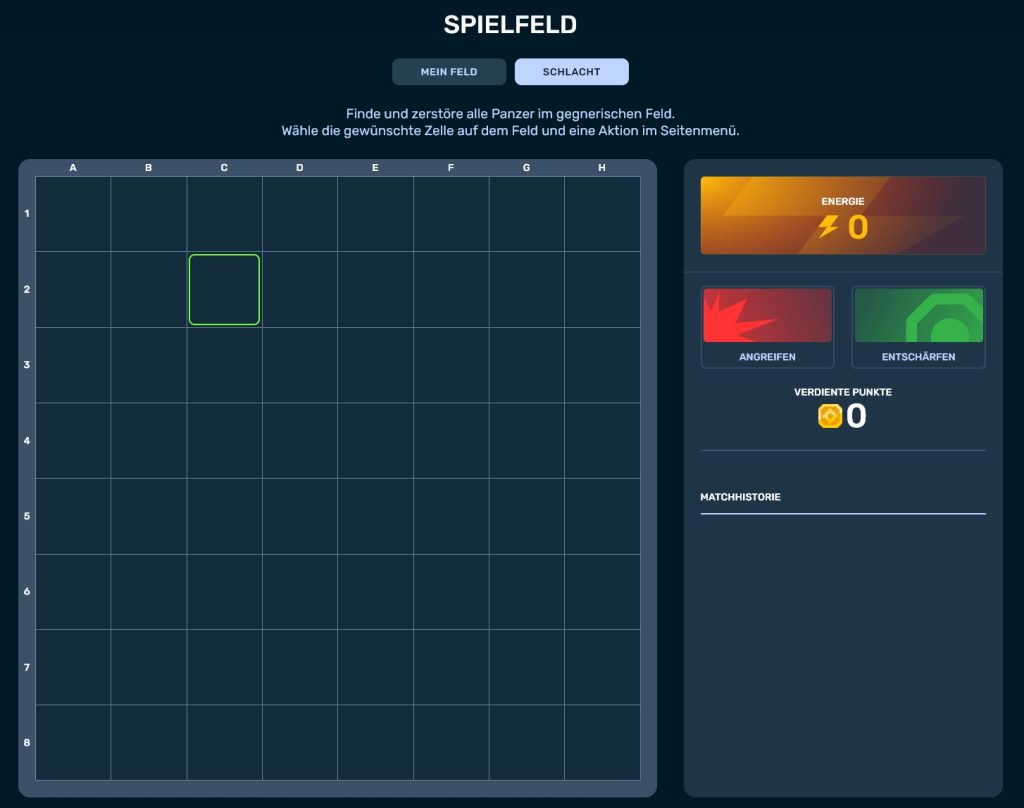
Ein neues Spielfeld erscheint unmittelbar nach einem Sieg.
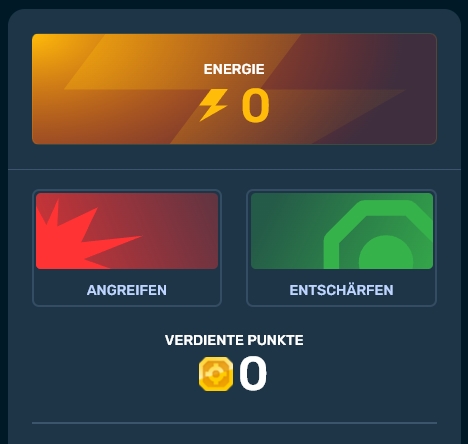
Auf diesem Spielfeld müsst Ihr alle gegnerischen Panzer finden und zerstören. Dazu könnt Ihr eine der folgenden Aktionen wählen:
- Angreifen – auf die ausgewählte Zelle schießen
- Entschärfen – das gesamte Feld von Minen befreien
Angreifen
- Um anzugreifen, müsst Ihr ein Quadrat auswählen und auf den “Angreifen”-Button drücken.
- Wenn Ihr ein Quadrat angegriffen habt, das Teil eines gegnerischen Panzers ist, wird keine Energie verbraucht.
- Falls Ihr verfehlt oder die Mine trefft, wird eine Einheit Energie verbraucht.
Entschärfen
Die Mine ist ein gefährliches Quadrat auf dem Spielfeld. Wenn Ihr sie trefft, verliert Ihr sofort 50% Eurer Gewinne. Um das zu verhindern, erhaltet Ihr den “Entschärfen”-Button. Bei Klick hierauf könnt Ihr das gesamte Spielfeld scannen und das Quadrat mit der Mine entschärfen! Ein Icon taucht auf dem Feld auf, woraufhin das Quadrat inaktiv wird und so keine Auswirkung mehr auf Euch haben kann!
Die Kosten der Entschärfung betragen 30 Rubine. Bei der Entschärfung wird keine Energie verbraucht.
Punkte

Im Falle eines Sieges (wenn Ihr also alle feindlichen Panzer zerstört habt) erhaltet Ihr 2 Punkte. Wenn Ihr eine Mine trefft, aber dennoch gewinnt, erhaltet Ihr 1 Punkt anstelle der gewöhnlichen 2.
Alle Punkte werden aufsummiert und können am Ende des Events für Preise im speziellen Event-Shop eingelöst werden.
Energie

Energie ist eine spezielle Event-Währung, die durch die Erfüllung von Kontrakten und speziellen Missionen erhalten werden kann.
Indem Ihr Energie verwendet, könnt Ihr gegnerische Panzer auf dem Spielfeld angreifen und so Event-Punkte verdienen.
Kontrakte

Ein Kontrakt ist eine Mission, in welcher Ihr Reputationspunkte in Matchmaking-Schlachten verdienen müsst.
Kontrakte können vom 3. Oktober bis zum 16. Oktober (jeweils 4 Uhr BZ) im Shop für Kristalle oder Rubine erworben werden.
Nach Kauf eines Kontraktes müsst Ihr diesen bei den Missionen im Abschnitt “Kontrakte” aktivieren.
Es gibt 2 Arten von Kontrakten im Spiel:

Belohnung: Energie ×3
Mehrfache Käufe möglich
- Zeit, die zum Abschluss zur Verfügung steht: 16. Oktober, 4 Uhr BZ
- Zeit, bis zu welcher der Preis eingesammelt werden kann: 16. Oktober, 4 Uhr BZ
- Alternative Belohnung, wenn nicht rechtzeitig abgeschlossen: 49900 Kristalle
- Alternative Belohnung, falls Belohnung nicht rechtzeitig eingesammelt wurde: 49900 Kristalle
- Vorzeitiger Abschluss: Statt Reputationspunkte zu verdienen, könnt Ihr die vorzeitige Fertigstellung des Kontraktes kaufen. Der Preis hierfür hängt von Eurem Fortschritt zum Beenden des Kontraktes ab.
- Kosten des Vorzeitigen Abschlusses: Zwischen 175 Rubinen und 1 Rubin

Belohnung: Energie ×15
Mehrfache Käufe möglich
- Zeit, die zum Abschluss zur Verfügung steht: 16. Oktober, 4 Uhr BZ
- Zeit, bis zu welcher der Preis eingesammelt werden kann: 16. Oktober, 4 Uhr BZ
- Alternative Belohnung, wenn nicht rechtzeitig abgeschlossen: 290 Rubine
- Alternative Belohnung, falls Belohnung nicht rechtzeitig eingesammelt wurde: 290 Rubine
- Vorzeitiger Abschluss: Statt Reputationspunkte zu verdienen, könnt Ihr die vorzeitige Fertigstellung des Kontraktes kaufen. Der Preis hierfür hängt von Eurem Fortschritt zum Beenden des Kontraktes ab.
- Kosten des Vorzeitigen Abschlusses: Zwischen 700 Rubinen und 1 Rubin
WICHTIGE Informationen:
- Ihr könnt nur 1 Kontrakt gleichzeitig aktiv haben.
- Wenn Ihr die Aufgabe des Kontrakts bereits erfüllt und 5000 Reputationspunkte verdient habt, solltet Ihr die Belohnung direkt abholen, da sonst kein neuer Kontrakt aktiviert werden kann.
- Wenn Ihr am Ende des Events einen Kontrakt abgeschlossen, aber seine Belohnung nicht abgeholt habt, erhaltet Ihr eine alternative Belohnung, die sich am Preis des Kontrakts orientiert.
Missionen
Um Energie zu erhalten, könnt Ihr außerdem Spezielle Missionen im Spiel abschließen, wodurch Ihr gegnerische Panzer auf dem Spielfeld angreifen und Event-Punkte verdienen könnt.
AUFGABE
Beende die Missionen «Windstille», «Sanfte Wellen», «Sturm», «Hurrikan» und «Tsunami».
BELOHNUNG
Erfahrungspunkte

Silber-Kontrakte
AUFGABE
Vernichte 1 Panzer mit Granaten in Matchmaking-Schlachten.
BELOHNUNG

Epischer Schlüssel
Erfahrungspunkte

Energie
AUFGABE
Vernichte 2 Panzer mit Granaten in Matchmaking-Schlachten.
BELOHNUNG

Epischer Schlüssel
Erfahrungspunkte

Energie
AUFGABE
Vernichte 3 Panzer mit Granaten in Matchmaking-Schlachten.
BELOHNUNG

Epischer Schlüssel
Erfahrungspunkte

Energie
AUFGABE
Vernichte 4 Panzer mit Granaten in Matchmaking-Schlachten.
BELOHNUNG

Epischer Schlüssel
Erfahrungspunkte

Energie
AUFGABE
Vernichte 5 Panzer mit Granaten in Matchmaking-Schlachten.
BELOHNUNG

Epischer Schlüssel
Erfahrungspunkte

Energie
Preise
Jetzt erzählen wir Euch von den Preisen!
Nachdem das Event vorbei ist, könnt Ihr Eure verdienten Punkte für Belohnungen im Event-Shop eintauschen.
Die Zahl der einlösbaren Punkte im Event-Shop ist auf 50 begrenzt. Nach Einlösung von 50 Punkten werden alle Preise bis auf Epische Schlüssel verborgen und sind nicht mehr zugänglich.
- Modul „Fuchs“
- Modul „Dachs“
- Modul „Ozelot“
- Modul „Wiesel“
- Modul „Wolf“
- Modul „Panther“
- Modul „Löwe“
- Modul „Delfin“
- Modul „Orka“
- Modul „Hai“
- Modul „Grizzly“
- Modul „Habicht“
- Modul „Falke“
- Modul „Geier“
- Modul „Eule“
- Modul „Adler“
- Variation „Kritische Mischung“ für Freeze
- Variation „Injektion von Schock-Nanobots“ für Isida
- Variation „Adaptives Nachladen“ für Hammer
- Variation „Hochkaliberkugeln“ für Hammer
- Variation „Blunderbuss“ für Hammer
- Variation „Revolver“ für Hammer
- Variation „Plasmatron“ für Twins
- Variation „Gummierte Projektile“ für Vulkan
- Variation „Großkaliber“ für Vulkan
- Variation „Schredder“ für Vulkan
- Variation „Hochgeschwindigkeitsmunition“ für Smoky
- Variation „Hochkalibermunition“ für Railgun
- Variation „Destabilisierte Geschosse“ für Railgun
- Variation „Kompulsive Anlage «Bote des Todes»“ für Railgun
- Variation „Hyperraumgeschosse“ für Railgun
- Variation „Excalibur-Schüsse“ für Railgun
- Variation „Hochgeschwindigkeitsmunition“ für Railgun
- Variation „Flintenmunition“ für Railgun
- Variation „Vakuum-Munition“ für Donner
- Variation „Nanotech-Munition“ für Donner
- Variation „Artifizielles Nachladen“ für Donner
- Variation „Bolter“ für Donner
- Variation „Amboss-Munition“ für Donner
- Variation „Uranium-Projektile“ für Skorpion
- Variation „Raketenwerfer «Tornado»“ für Skorpion
- Variation „Raketenwerfer «Schwarm»“ für Skorpion
- Variation „Minenwerfer“ für Magnum
- Variation „Zerstörer“ für Magnum
- Variation „Nemesis“ für Gauß
- Variation „Solenoid-Kühlung“ für Gauß
- Variation „Hochgeschwindigkeitsmunition“ für Gauß
- Seltener Schlüssel
- Epischer Schlüssel
- Legendärer Schlüssel
Viel Glück, habt Spaß, und möge der Stärkste gewinnen!
Das Event wird von der APL Publishing Ltd. in Übereinstimmung mit den Allgemeinen Regeln der Durchführung der Aktionen und Wettkämpfe veranstaltet.

Wenn Ihr Euch noch nicht sicher seid, ob Ihr an Turnieren teilnehmen wollt oder nicht, dann ist jetzt der richtige Zeitpunkt für eine Entscheidung! Das eSport-Format der Ranking-Turniere soll die Teilnahme erleichtern, sodass jeder eine Chance hat, um die beeindruckenden Ingame-Belohnungen und sogar Echtgeld zu kämpfen!
Wer weiß, vielleicht werden es Du und Dein Team sein, die das beste Ergebnis erzielen!
Wir wollen Euch auch daran erinnern, dass wir zur Vereinfachung der Suche nach Spielern und Teams die eSports-Webseite überarbeitet haben. In einem neuen, speziellen Abschnitt können Teams Spieler suchen und Spieler Teams
Turnier-Regeln
- Ränge: Stabsunteroffizier bis Legende
- Die Teams bestehen aus 7 Spielern
- In der Schlacht sind 5 Spieler aus jedem Team
- Eure Garage ist nicht wichtig, da die Schlachten im Sport-Format ausgetragen werden.
- Auf dem Schlachtfeld dürfen die Untersätze und Waffen in jedem Team nicht doppelt vorkommen. Wenn Ihr zum Beispiel Hornet und Ricochet tragt, darf niemand sonst aus Eurem Team mit Ricochet oder Hornet in der Schlacht sein.
- Detaillierte Regeln findet Ihr auf der Turnier-Seite im eSports-Portal.
Preise
- Rating-Punkte
- Die einzigartige Farbe “Säure”
- 96.000 Tankoins
- 88.000.000 Kristalle
- 2.835 epische Schlüssel
- 1.071 Tage Premium-Account
Turnier-Daten
- Die Anmeldung für das Turnier dauert vom 23. September um 19 Uhr BZ bis zum 6. Oktober 19 Uhr BZ
- Das erste Match startet am 7. Oktober
- Das Turnier wird vor dem 29. Oktober enden
- Die Transfers sind bis zum 6. Oktober um 19 Uhr BZ geöffnet
Am Turnier werden 32 bis 128 Teams teilnehmen.
Nach dem dritten Rating-Turnier werden wir das Hauptturnier ankündigen. Dort wird nicht nur um Ingame-Belohnungen gekämpft, sondern auch um Echtgeld.
Geht zum eSports-Portal, erstellt ein Team, lest die Regeln, meldet Euch an und macht Euch bereit für das dritte Rating-Turnier! Und wenn Ihr irgendwelche Fragen habt, besucht unseren eSports-Discordserver, dort erhaltet Ihr definitiv Hilfe.
Wir sehen uns auf dem Schlachtfeld und in den eSports-Übertragungen!

Event-Daten: vom 26. September bis zum 17. Oktober (jeweils 4 Uhr BZ).
Rabatte
Profitiert von großartigen Rabatten, die es vom 26. September bis zum 29. September geben wird!
Für drei ganze Tage könnt Ihr folgende Gegenstände 30% günstiger erhalten:
Spezielle Event-Modi
Drei spannende Spielmodi erwarten Euch im Spiel!
Die Hauptaufgabe besteht darin, alle Gegner zu „bonken“, Punkte zu erobern und sie für einen schnellen Sieg so lange wie möglich zu kontrollieren.
- Sandkasten (REMASTER)
- Forest (REMASTER)
- Sandal (REMASTER)
- Parma (REMASTER)
Vernichtet im DM-Modus alles in Eurem Weg und fangt viele Goldboxen, denn ihre Abwurfrate ist in diesem Modus erhöht!
- Bobruisk MM
- Brücken MM
- Molotow MM
- Tribut MM
Im Spielmodus „Sumo“ beherrscht jeder Panzer die antike Kunst des Sumo: Spieler kämpfen in Schwergewicht-Mammut-Untersätzen und tragen eine verbesserte Version der Waffe „Hammer“. Nahkämpfe werden der Schlüssel zum Sieg – drückt Eure Gegner mit purer Masse und Stärke weg, im Stile der Sumo-Kämpfe. Trefft Euch in epischen Duellen, in welchen nur jene, die standhaft sind, überleben. Taucht in Schlachten ein, wo jeder Schlag Euch näher zum Triumph bringt!
- Bauernhof PRO
- Erdhügel PRO
- Magadan PRO
- Welle PRO
Sonderangebote
Was wäre ein Feiertag ohne einige tolle Angebote zu großartigen Preisen?
26. September — 13. Oktober:

26. September — 17. Oktober:


** Kommt in den nächsten 30 Tagen ins Spiel, um täglich eine abgeschlossene Spezialmission zu erhalten. Sammelt sie ein und erhaltet jeweils 150 Rubine.
Das Angebot kann nur einmal gekauft werden.





3. Oktober — 17. Oktober:



10. Oktober — 17. Oktober:

Epische Container

- SKIN Stürmer UT
- SKIN Hunter UT
- Variation “Raketenwerfer «Meteor»” für Stürmer
- Variation “Atomraketen” für Stürmer
- Variation “Raketenwerfer «Hydra»” für Stürmer
- Variation “Lebensretter” für Hunter
- Variation “Excelsior” für Hunter
- Und alles, was Ihr auch aus Gewöhnlichen Containern erhalten könnt
Spezielle Missionen
Wir haben Euch eine Fülle an spannenden Missionen vorbereitet, welche das Event noch aufregender machen werden!
Teil 1: 26. September — 3. Oktober
Teil 2: 3. Oktober — 10. Oktober
Teil 3: 10. Oktober — 17. Oktober
AUFGABE
Beende 1 Schlacht im Gewinnerteam in Matchmaking-Schlachten.
WICHTIG: Diese Mission ist nur für Spieler mit Premium-Account verfügbar.
BELOHNUNG

EPISCHER SCHLÜSSEL
AUFGABE
Beende 3 Schlachten in Matchmaking-Schlachten.
WICHTIG: Diese Mission ist nur für Spieler mit Schlacht-Abonnement verfügbar.
BELOHNUNG

EPISCHER SCHLÜSSEL
AUFGABE
Erspiele 500 Reputationspunkte im festlichen Modus „Schlachter“.
BELOHNUNG

EPISCHER SCHLÜSSEL
AUFGABE
Beende 1 Schlacht im Gewinnerteam in Matchmaking-Schlachten.
WICHTIG: Diese Mission ist nur für Spieler mit Premium-Account verfügbar.
BELOHNUNG

EPISCHER SCHLÜSSEL
AUFGABE
Beende 3 Schlachten in Matchmaking-Schlachten.
WICHTIG: Diese Mission ist nur für Spieler mit Schlacht-Abonnement verfügbar.
BELOHNUNG

EPISCHER SCHLÜSSEL
AUFGABE
Erspiele 500 Reputationspunkte im festlichen Modus „Goldjäger“.
BELOHNUNG

EPISCHER SCHLÜSSEL
AUFGABE
Beende 1 Schlacht im Gewinnerteam in Matchmaking-Schlachten.
WICHTIG: Diese Mission ist nur für Spieler mit Premium-Account verfügbar.
BELOHNUNG

EPISCHER SCHLÜSSEL
AUFGABE
Beende 3 Schlachten in Matchmaking-Schlachten.
WICHTIG: Diese Mission ist nur für Spieler mit Schlacht-Abonnement verfügbar.
BELOHNUNG

EPISCHER SCHLÜSSEL
AUFGABE
Erspiele 500 Reputationspunkte im festlichen Modus „Sumo“.
BELOHNUNG

EPISCHER SCHLÜSSEL
26. September — 17. Oktober
AUFGABE
Beende die Missionen «Willkommen! Teil 1», «Eine Frage der Ehre. Teil 1», «Wahl ohne Wahl. Teil 1», «Melancholie. Teil 1», «Teil des Teams. Teil 1», «Freuden des Lebens. Teil 1», «Warmes Plätzchen», «Regenerator», «Allee der Sterne», «Präventivspiel» und «7 Tage. Teil 1».
BELOHNUNG

EPISCHER SCHLÜSSEL

SELTENER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Betrete das Spiel mindestens einmal.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Erspiele 5000 Reputationspunkte in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Erspiele 3000 Reputationspunkte im Modus „Schnelle Schlacht“ in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Beende 10 Schlachten in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Beende 2 Schlachten im Gewinnerteam in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Kaufe einen beliebigen Gegenstand im Shop des Spiels.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Erspiele 1000 Reputationspunkte im Modus „Control Points“ in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Benutze 150 mal Reparaturkiste in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Erspiele 45 Sterne in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Vernichte 1 Panzer mit Granaten in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Beende 3 Wöchentliche Missionen.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
3. Oktober — 17. Oktober
AUFGABE
Beende die Missionen «Willkommen! Teil 2», «Eine Frage der Ehre. Teil 2», «Wahl ohne Wahl. Teil 2», «Melancholie. Teil 2», «Teil des Teams. Teil 2», «Freuden des Lebens. Teil 2», «Weitwurf», «Nicht runterschauen», «Tödliche Aussaat», «Goldreserve» und «Herbst-Exazerbation».
BELOHNUNG

EPISCHER SCHLÜSSEL

SELTENER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Betrete das Spiel mindestens einmal.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Erspiele 5000 Reputationspunkte in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Erspiele 3000 Reputationspunkte im Modus „Schnelle Schlacht“ in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Beende 10 Schlachten in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Beende 2 Schlachten im Gewinnerteam in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Kaufe einen beliebigen Gegenstand im Shop des Spiels.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Erspiele 1000 Reputationspunkte im Modus „Rugby“ in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Benutze 150 mal Minen in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Benutze 10 mal in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Verdiene 4000 Kristalle in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Benutze 10 mal den Overdrive in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
10. Oktober — 17. Oktober
AUFGABE
Beende die Missionen «Willkommen! Teil 3», «Eine Frage der Ehre. Teil 3», «Wahl ohne Wahl. Teil 3», «Melancholie. Teil 3», «Teil des Teams. Teil 3», «Freuden des Lebens. Teil 3», «Teamspieler», «Wut», «Metzger», «Tageszeit» und «7 Tage. Teil 2».
BELOHNUNG

EPISCHER SCHLÜSSEL

SELTENER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Betrete das Spiel mindestens einmal.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Erspiele 5000 Reputationspunkte in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Erspiele 3000 Reputationspunkte im Modus „Schnelle Schlacht“ in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Beende 10 Schlachten in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Beende 2 Schlachten im Gewinnerteam in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Kaufe einen beliebigen Gegenstand im Shop des Spiels.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Erspiele 1000 Reputationspunkte im Modus „Team Deathmatch“ in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Benutze 150 mal Schadensverstärker in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Vernichte 30 Panzer in Matchmaking-Schlachten.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Beende 15 Tägliche Missionen.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
AUFGABE
Beende 3 Wöchentliche Missionen.
BELOHNUNG

GEWÖHNLICHER SCHLÜSSEL
ERFAHRUNGSPUNKTE
Adventskalender
Wir starten den festlichen Adventskalender für Euch!
Nachdem Ihr das Sonderangebot “Adventskalender” gekauft habt, bekommt Ihr Zugang zu:
- 5 Standardmissionen
- 1 Supermission mit einzigartigen Belohnungen!
Anschließend müsst Ihr Euch nur während des Events im Spiel einloggen und Eure Geschenke abholen.
Aufgabe: Beendet alle “Ein weiterer Tag”-Missionen, die nach dem 26. September erscheinen.
Das Beenden von 5 Standardmissionen schaltet die finale Supermission frei.
Supermission


Ein weiterer Tag


Elite-Pass
Der luxuriöseste Pass kommt zurück ins Spiel! Er wird aus 20 Stufen bestehen.
Euer Ziel ist, Sterne zu verdienen und neue Level freizuschalten. Für jedes Level erhaltet Ihr neue Preise. Um den gesamten Pass abzuschließen und den Hauptpreis zu erreichen, müsst Ihr 1000 Sterne verdienen. Ihr habt bis zum Ende des Events Zeit, um den Pass abzuschließen.

Wichtig: Alle während des Events verdienten Sterne werden gezählt. Der Fortschritt beginnt mit dem Beginn des Events. Angerechnet werden auch die vor dem Kauf des “Elite-Passes” gesammelten Sterne. Der “Elite-Pass” wird benötigt, um die Preise zu erhalten. Wenn Ihr ihn kauft, erhaltet Ihr alle freigeschalteten Preise!
Die Hauptpreise dieses Elite-Passes sind ein Legendärer Schlüssel und die Variation “Excelsior” für Stürmer!
Der Preis für den Elite-Pass beträgt 2300 Rubine.
Festliche Dekorationen
- Festliche Lieferdrohnen
- Feiertagsfarbe
- Festliche Goldbox-Dropzonen
- Festlicher Ladebildschirm
- Festliche Werbetafeln
- Rote Apfel-Goldbox

Wir wünschen allen einen hellen Herbst und nichts als Siege in Tanki Online!

Was ist Parkour Survival?
Parkour Survival ist der ultimative teambasierte Parkour-Wettbewerb in Tanki Online. Stellt eine Gruppe von bis zu 5 Mitgliedern zusammen und geht eine Serie von immer schwieriger werdenden Herausforderungen an. Ab dem 15. August wird jede Woche eine neue Parkour-Herausforderung veröffentlicht. Wenn Ihr sie schafft, rückt Euer Team zur nächsten Herausforderung vor. Wenn Ihr scheitert, seid Ihr raus. Nur die stärksten, kreativsten und hartnäckigsten Teams werden bis zum Ende durchhalten können.
Wie man teilnimmt
Es ist keine Anmeldung nötig! Der Beitritt erfolgt folgendermaßen:
- Stellt ein Team von (maximal) 5 Teilnehmern zusammen.
- Jeder Teilnehmer soll die Farbe “Blaze” in der Garage kaufen und während der Ausführung der Tricks tragen.
- Besucht die Event-Website am 15. August, lest die Regeln der ersten Herausforderung (am 15. August veröffentlicht) und erledigt sie.
- Ladet ein Video auf YouTube hoch, welches das erfolgreiche Absolvieren der Herausforderung durch Euer Team zeigt.
- Sendet den Video-Link im Bereich der Herausforderungen auf der Event-Website unter Angabe Eures Team-Namens und Eurer Mitglieder ein.
- Das war’s! Euer Team ist offiziell eingeschrieben.
- Wartet auf die Ergebnisse der ersten Herausforderung. Wenn Euer Team diese geschafft hat, könnt Ihr Euch an der nächsten Herausforderung versuchen.

Diese Farbe gehört zu den furchterregenden Spielern der Parkour-Community, welche alle grauenhaften Herausforderungen von Parkour Survival bestanden und den Wettbewerb als einzelnes Team beendet haben.
Während des Turniers kann diese Farbe in der Garage gekauft werden. Nach dem Turnier besitzen diese Farbe nur die Gewinner.
Herausforderungen
Es gibt insgesamt 8 verschiedene Herausforderungen. Jede beginnt erst dann, wenn die vorherige Herausforderung vorbei ist.
| Herausforderung | Startdatum | Enddatum |
| 1 | 15.08 | 29.08 |
| 2 | 29.08 | 05.09 |
| 3 | 05.09 | 12.09 |
| 4 | 12.09 | 19.09 |
| 5 | 19.09 | 26.09 |
| 6 | 26.09 | 3.10 |
| 7 | 3.10 | 10.10 |
| 8 | 10.10 | 17.10 |
Preise
Euer Aufwand wird natürlich belohnt: Erhaltet Preise für jede absolvierte Herausforderung, darunter Schlüssel, Rubine sowie die exklusive Farbe “Blaze”.
Exklusive Farbe “Blaze”: Nur die Teams, welche es schaffen, alle 8 Herausforderungen zu meistern, erhalten dieses legendäre Ehrenabzeichen. Die Farbe bleibt auf deren Accounts bis zum nächsten Turnier oder bis die Administration eine anderslautende Entscheidung trifft.
Preise für jedes Mitglied eines Teams:
Herausforderung 1


Herausforderung 2


Herausforderung 3


Herausforderung 4


Herausforderung 5


Herausforderung 6


Herausforderung 7


Herausforderung 8




Teams, die eine Herausforderung schaffen, erhalten ihre Belohnungen innerhalb von drei Werktagen nach dem Ende der Herausforderung.
Seid Ihr bereit für den Survival-Kampf? Stellt Euer Team zusammen, schärft Eure Skills und bereitet Euch auf den ultimativen Parkour-Showdown vor!
Parkour Survival 2025 beginnt bald — wird Euer Team der letzte Überlebende sein?
Informiert Euch regelmäßig für Neuigkeiten – lasst die Herausforderungen beginnen!
 Jump to content
Jump to content

Empfohlene Beiträge